L-Py Turtle basic primitives¶
The L-string can be parsed and its modules can be interpreted as commands for a 3D turtle. A number of basic primitives that are understood by the turtle are explained in this page :
| F | width (!) | rotation (/) | MoveTo | nF |
| f | color (;) | rotation (\) | MoveRel | LineTo |
| @O | color (;) | rotation (^) | Pinpoint | LineRel |
| @o | setColor | rotation (&) | PinpointRel | OLineTo |
| @B | branching ([]) | rotation (+) | setHead (@R) | OLineRel |
| @b | polygons (.) | rotation (-) | EulerAngles | SetGuide |
| width (_) | Frame | Rescaling | generalisedCylinders (@Gc and @Ge) |
Constructing basic shapes with the Turtle¶
Simple Turtle instructions¶
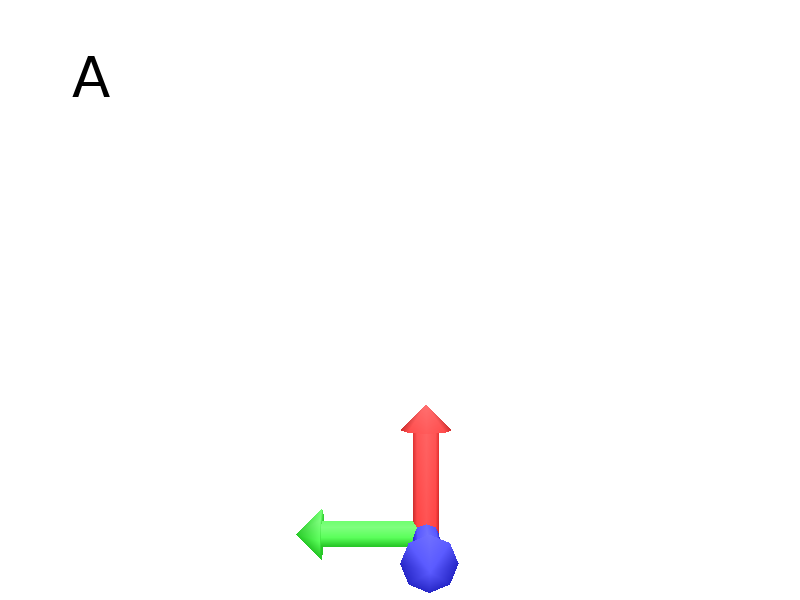
The Turtle is a geometric tool defined by a reference frame that can be moved and oriented in space using a number of instructions. As an illustration the following examples shows how the F primitive can be used to draw cylinders and + to rotate counterclockwise.
#Turtle initial position (Fig. A)
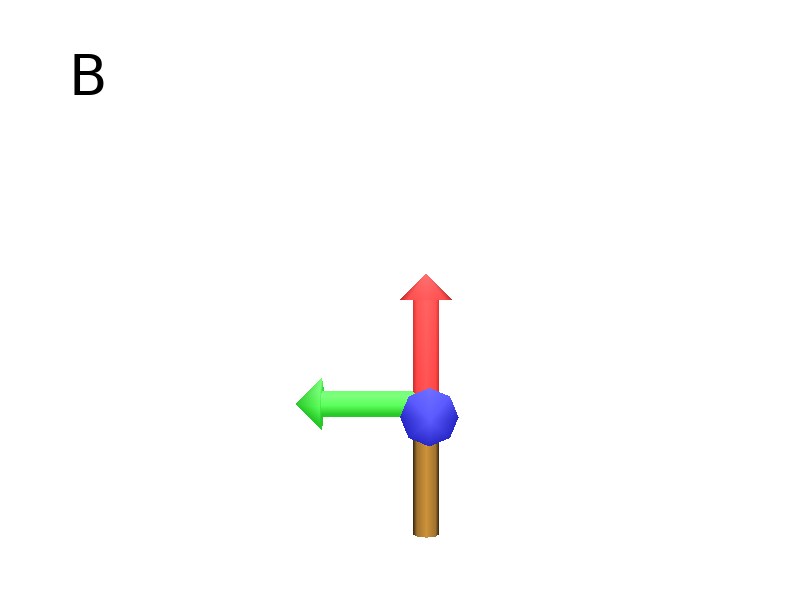
Axiom: F #(Fig. B)
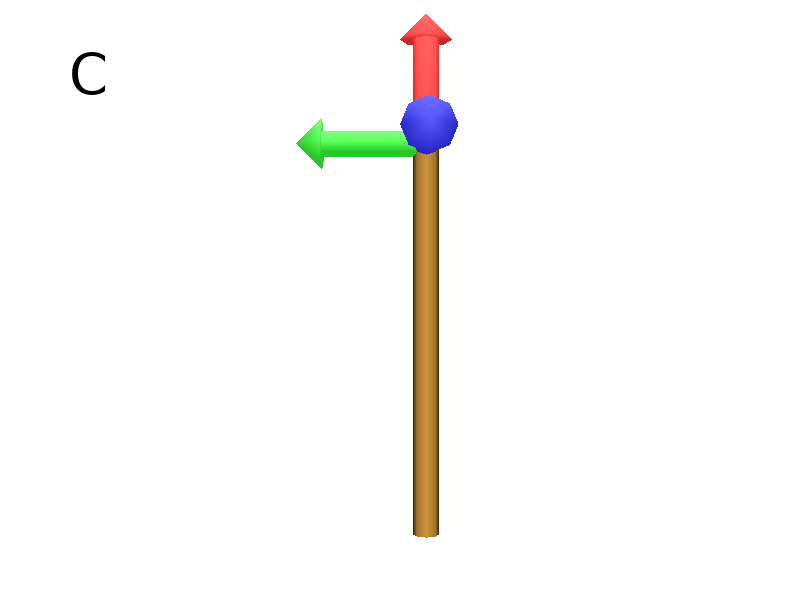
Axiom: FFF #(Fig. C)
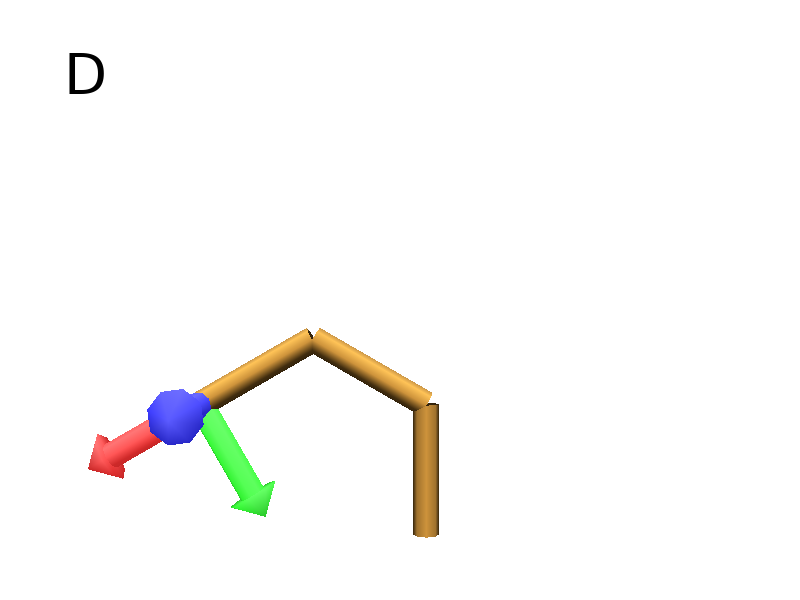
Axiom: F+F+F #(Fig. D)
|
|
|
|
Axiom: F+F-F #(Fig. A)
Axiom: FF-(90)FF-(90)FF-(90)FF #(Fig. B)
Axiom: FF[-F][+F]F #(Fig. C)
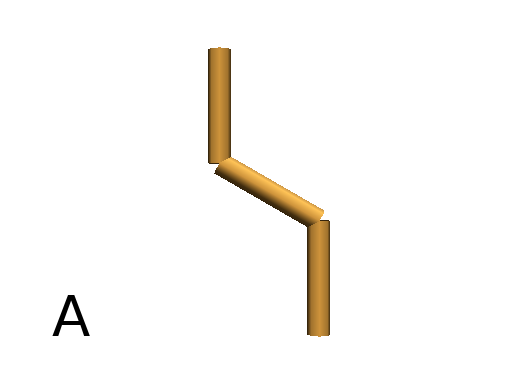
|

|
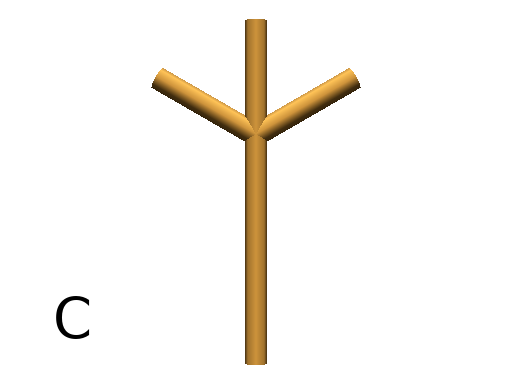
|
The F primitive moves the Turtle and draws a cylinder of one unit.
To move the Turtle without drawing something, f should be used.
Axiom: F[+fF]F[-fF]FF #(Fig. A)
Axiom: +(90)F-(45)f-(45)F-(45)f-(45)F-(45)f-(45)F #(Fig. B)
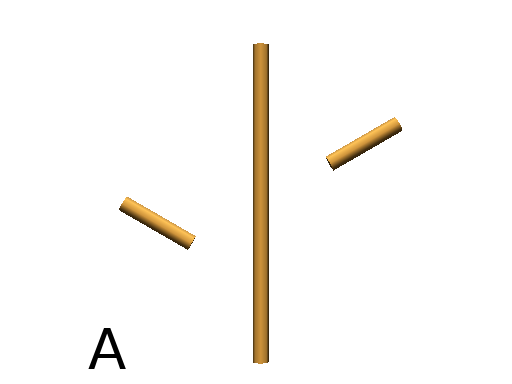
|
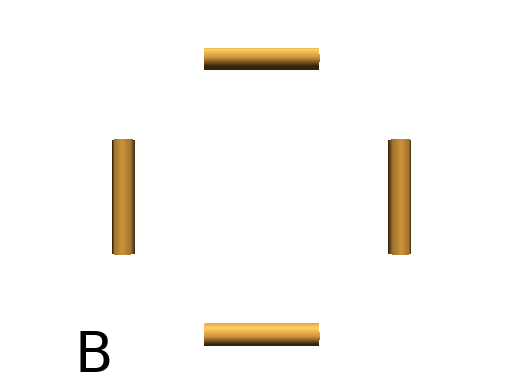
|
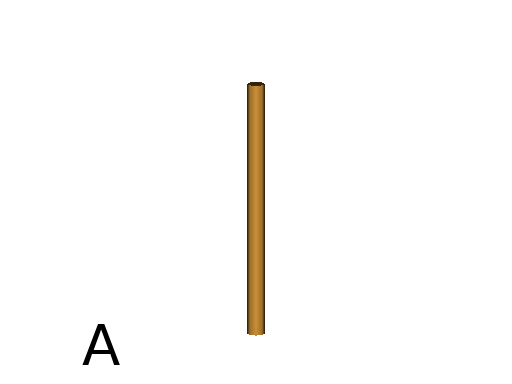
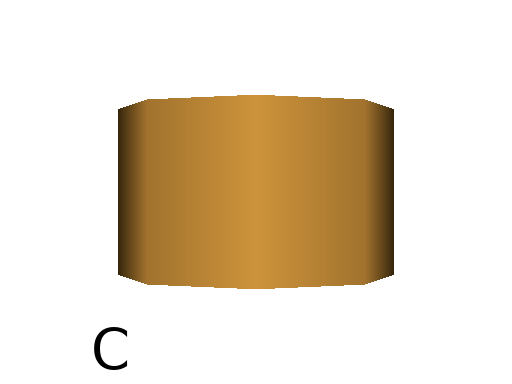
F can take arguments (of type float). The first argument defines the length of the cylinder (default value = 1). By default, the radius of the cylinder is by set to 0.1.
Axiom: F(3) #(Fig. A)
Second argument defines the radius at the top of the cylinder (the bottom radius being defined by the current width value of the Turtle state)
Axiom: F(3, 2.5) #(Fig. B)
To change the value of the Turtle’s width before applying the F command, the _ primitive can be used:
Axiom: _(2.5)F(3, 2.5) #(Fig. C)
|
|
|
Similarly, the + symbol specifies a rotation whose angle is given by its first parameter.
Other basic geometric primitives make it possible to draw other predifined shapes :
Axiom: @O(1) # Draws a sphere at the Turtle's position.
# It can take one argument which is the radius of the sphere.
Axiom: @o(1) # Draws a circle at the Turtle's position.
# It can take one argument which is the radius of the circle.
Axiom: @B(1) # Draws a box at the Turtle's position.
# It can take two arguments which are the length of the edges and the topradius.
Axiom: @b(1) # Draws a quad at the Turtle's position.
# It can take two arguments which are the length of the edges and the topradius.
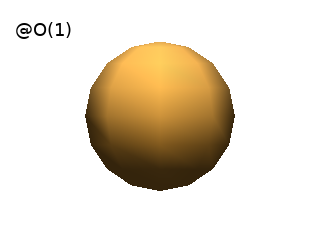
|
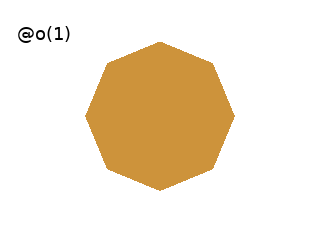
|
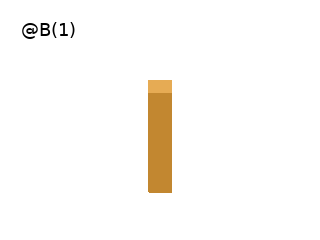
|
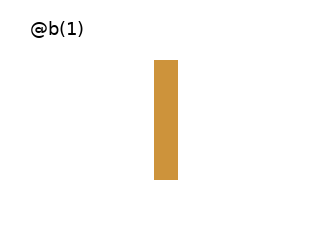
|
Text can be displayed using the @L primitive.
Axiom: @L("Some text", 18) # Draws a text Label at the Turtle's position.
# It can take two arguments which are the text to display and it's size.
Controling width and color of primitives¶
Changing the width¶
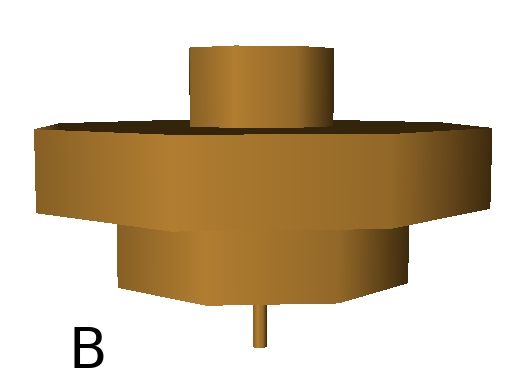
The width of the shapes can be increased (resp. decreased) using _ (resp. !). These primitives increment or decrement width by 1. The default width is 0.1.
Axiom: F_ _ _F!F!F # At the beginning, the cylinder has a width of 0.1 (default) then 3.1, then 2.1 and finally 1.1 (Fig. A)
|
|
Alternatively, the width can be set using setWidth or by giving argument to _ or !
Axiom: F_(2)F!(3)F!(1)F # (Fig. B)
Download the example : width.lpy
Color System¶
To use color system, it is necessary to set materials with the Color Map window (Color Map).
The semicolon (‘;’) is used to increase the current material index (Fig. A) and the comma (‘,’) to decrease it (Fig. B). A argument can be set to specify the index of the material to use.
Axiom: F(2) ; @O(0.2) # (Fig. A)
# Or equivalently:
Axiom: F(2) ;(2) @O(0.2)
Axiom: F(2) , @O(0.2) # (Fig. B)
# Or equivalently:
Axiom: F(2) ,(0) @O(0.2)
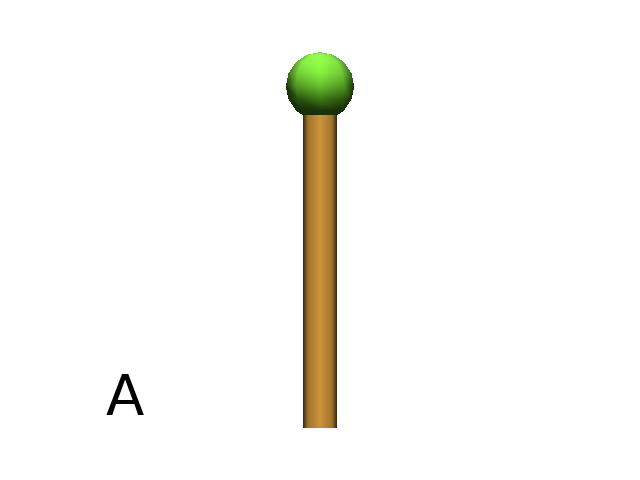
|
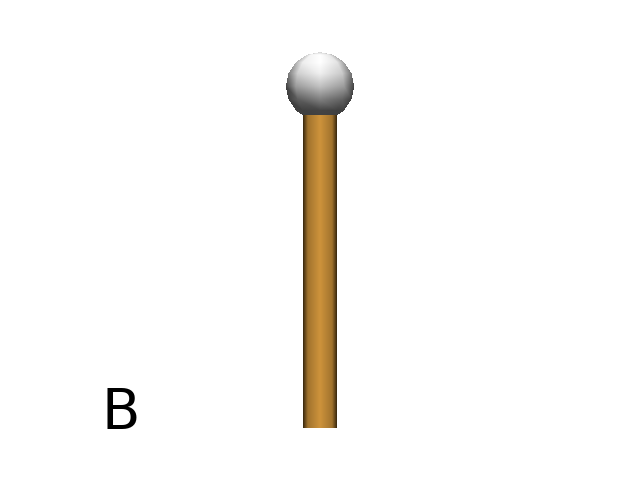
|
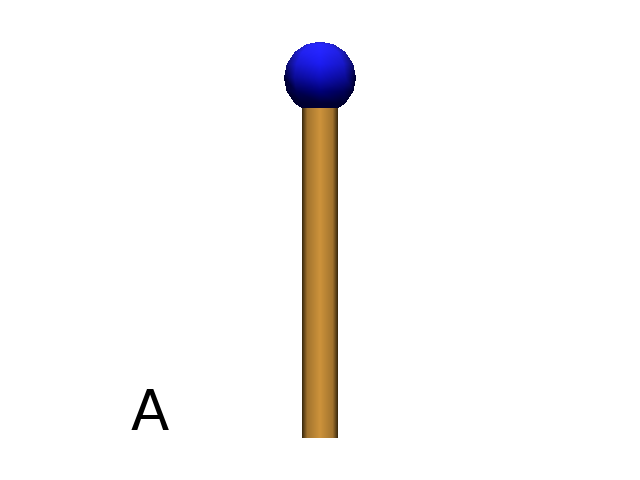
The SetColor primitive allow you to specify the appearance of the next primitive drawn by the turtle using either an index in the Color Map or directly using red, green, blue (or rgba) values as arguments (Fig. B). It is also possible to pass directly a plantgl Material object to specify a more complex appearance.
Axiom: F(2) SetColor(5) @O(0.2) # (Fig. A)
Axiom: F(2) SetColor(45, 200, 200) @O(0.2) # (Fig. B)
|
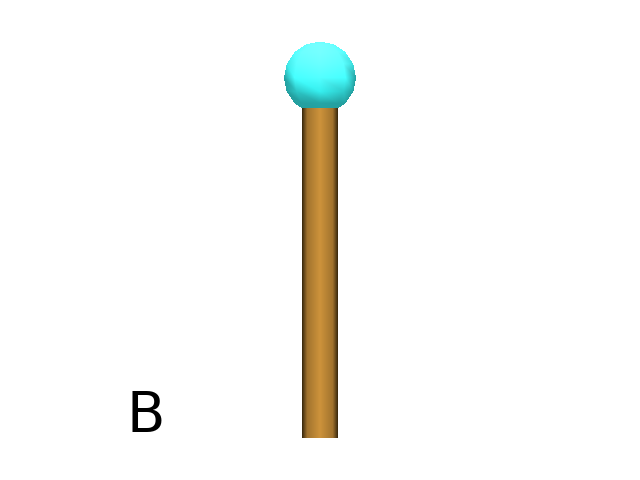
|
Drawing more complex shapes¶
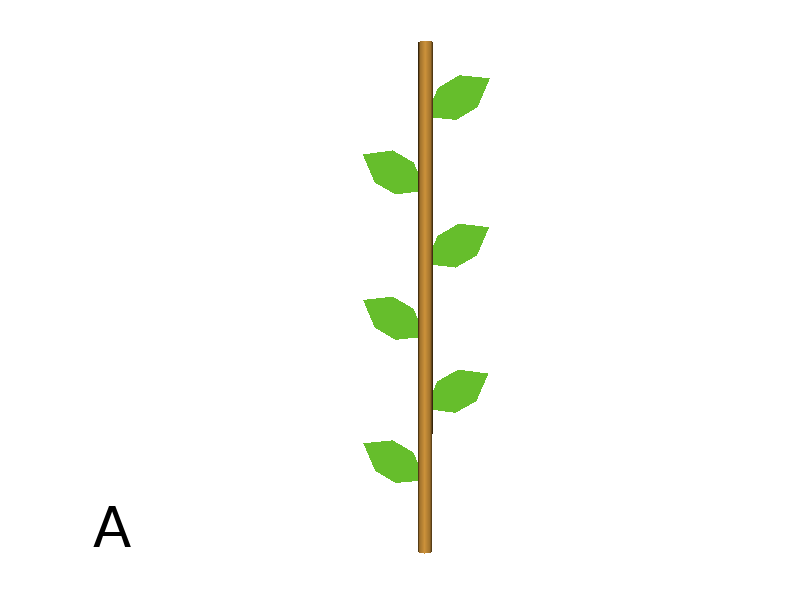
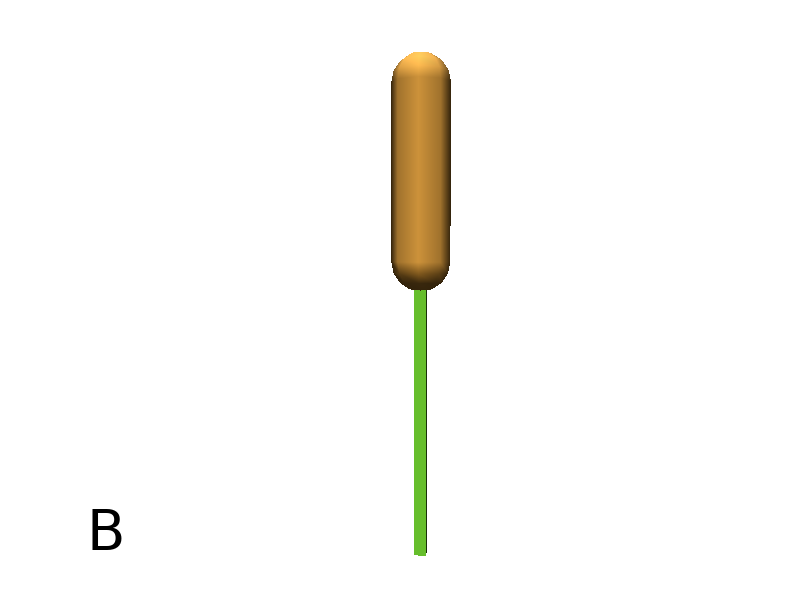
Specific shapes can be drawn using ~. A predefined leaf shape is availabled using ~l.
Axiom: F[;+~l]F[;-~l]F[;+~l]F[;-~l]F[;+~l]F[;-~l]F #(Fig. A)
Axiom: ;@B(5),@O(0.5)_(0.5)F(3,0.5)_(0.2)@O(0.5) #(Fig. B)
Download the example : combined.lpy
|
|
In order to draw complex shapes, some basic knowledge about the Turtle is required.
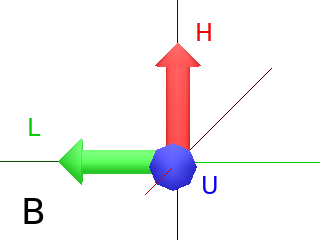
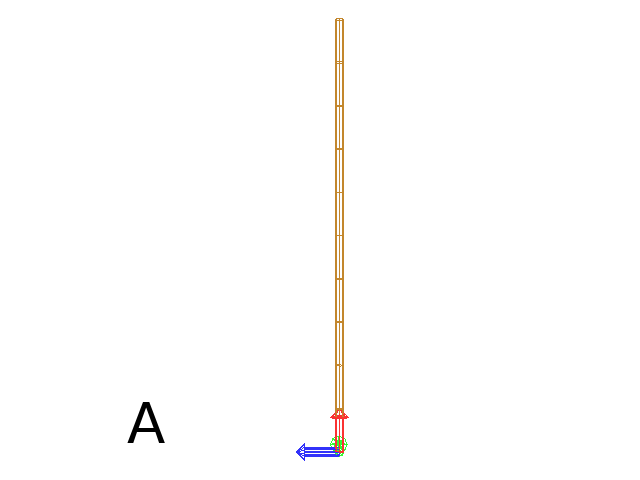
Definition of the Turtle’s reference frame (HLU)¶
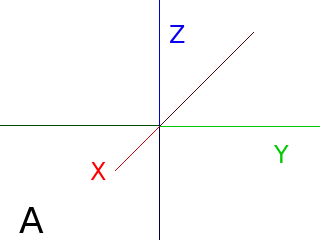
In L-Py, screen coordinates are defined in a global reference frame F0 = (X,Y,Z) of L-Py (Fig. A).
The Turtle is defined by a reference frame (H,L,U) with respect to F0 (Fig. B) and can be displayed using the primitive Frame
- H (Head) pointing in the direction of the Turtle’s “head”.
- L (Left) pointing in the direction of the Turtle’s “left arm”.
- U (Up) pointing in the direction of for the Turtle’s back (“up”).
Axiom: Frame
|
|
Rotating with HLU (Main primitives)¶
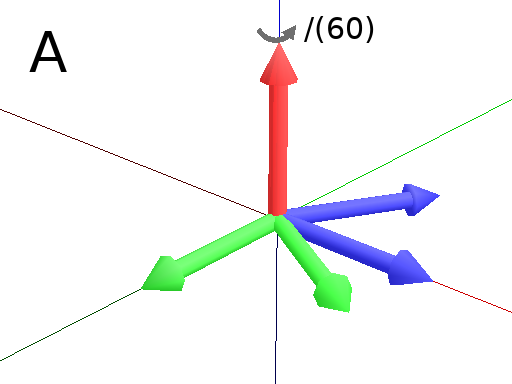
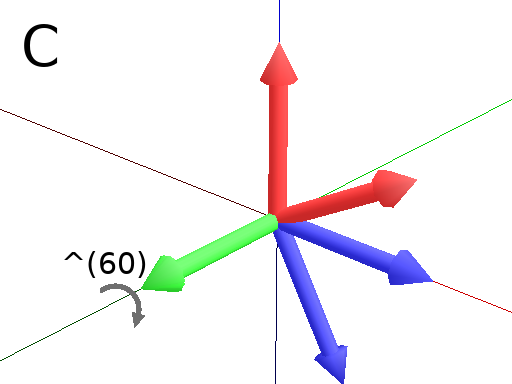
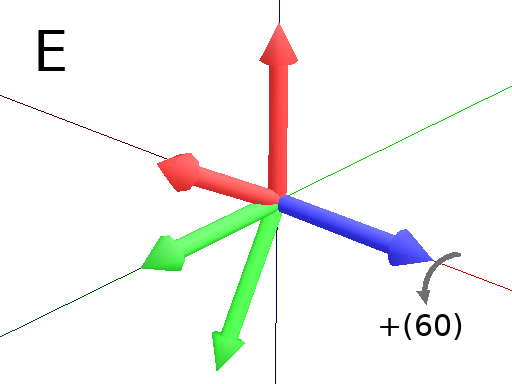
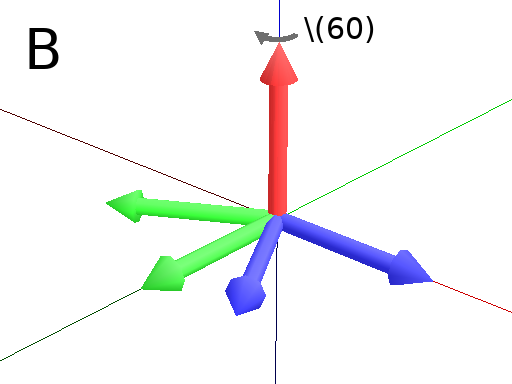
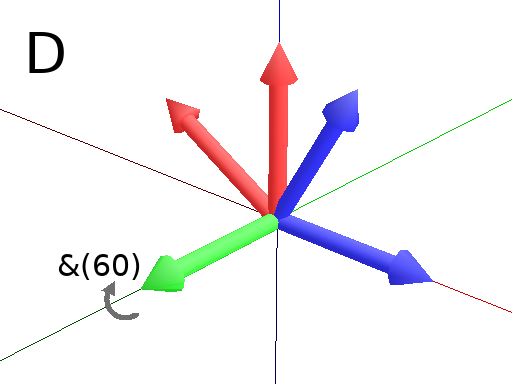
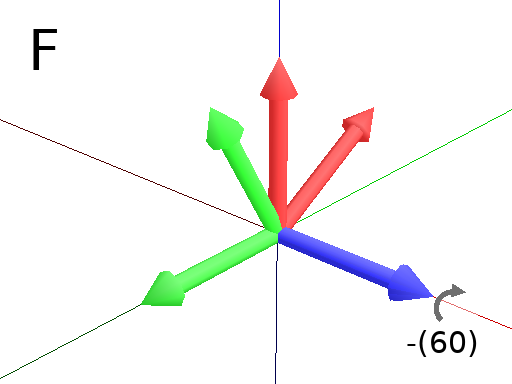
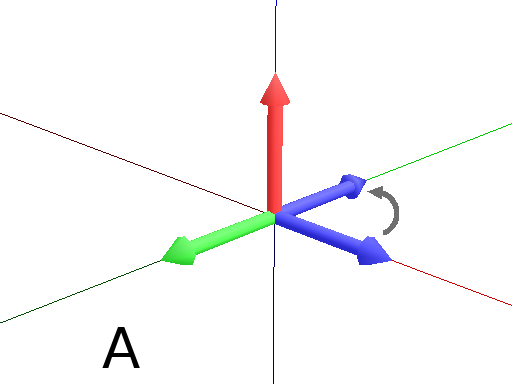
Primitives can be used to rotate the Turtle in its current reference frame (H = Head, L = Left, U = Up, angles are expressed by default in degrees). These primitives are paired (one and it’s opposite) : / and \, ^ and & and finally + and -.
Axiom: Frame(2) /(60) Frame(2) # Roll left arround the H axis. (Fig. A)
Axiom: Frame(2) \(60) Frame(2) # Roll right arround the H axis. (Fig. B)
Axiom: Frame(2) ^(60) Frame(2) # Pitch up arround the L axis. (note that the rotation is indirect) (Fig. C)
Axiom: Frame(2) &(60) Frame(2) # Pitch down arround the L axis. (note that the rotation is indirect) (Fig. D)
Axiom: Frame(2) +(60) Frame(2) # Turn left arround the U axis. (Fig. E)
Axiom: Frame(2) -(60) Frame(2) # Turn right arround the U axis. (Fig. F)
Download the example : rotation.lpy
|
|
|
|
|
|
Rescaling the Turtle¶
Three primitives can be used to rescale the Turtle : SetScale, DivScale and MultScale (shorter symbols are @D, @Dd and @Di respectively) SetScale sets the scale to the value in argument. DivScale (resp. MultScale) divides (resp. multiplies) the current scale by the value given in argument. The first image is the initial shape (Fig. A) and the second one is the same shape where the branches are rescaled (Fig. B).
Axiom: FF[-F[-F]F]FF #(Fig. A)
Axiom: @D(2)FF[@Dd(1.5)-F[@Di(0.5)-F]F]FF #(Fig. B)
Download the example : scale.lpy
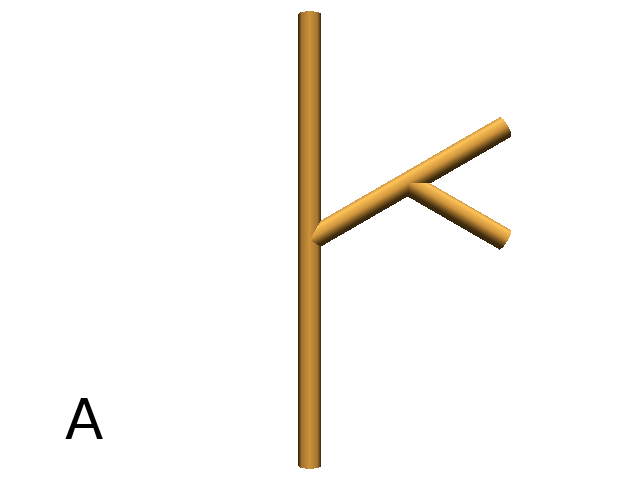
|

|
How to draw polygonal shapes ?¶
Basic method¶
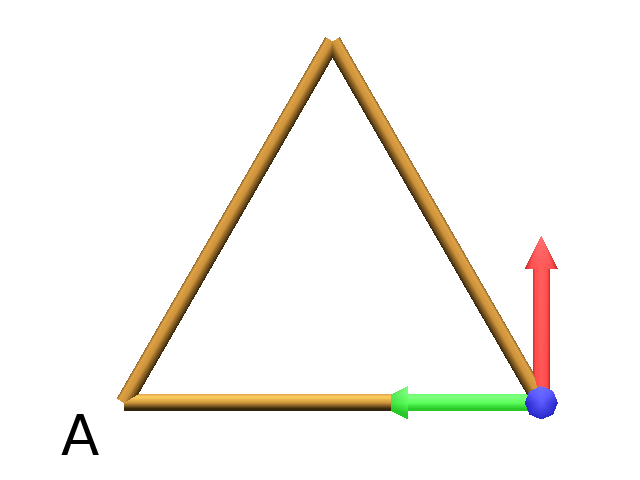
Turn and move forward : Here, at each +, the Turtle does a rotation of the number of degrees indicated in arguments arround the U axis
Axiom: Frame(2)+(30)F(5)+(120)F(5)+(120)F(5) # (Fig. A)
Download the example : polygons.lpy
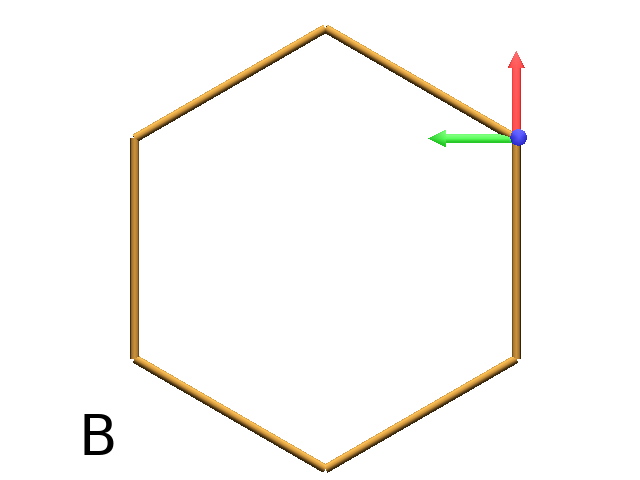
Procedural method¶
A loop construct can be used to produce the L-string specifying the polygon
Axiom: Frame(2)+F(5)+F(5)+F(5)+F(5)+F(5)+F(5) # (Fig. B)
# Or equivalently:
Axiom:
nproduce Frame(2)
for i in range(6):
nproduce +F(5)
|
|
Filled polygons¶
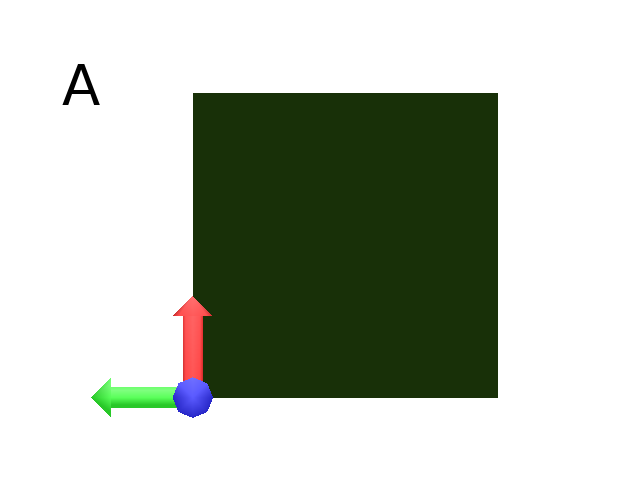
Polygon can be drawn by using {} and positioning a series of dots (‘.’) in space, corresponding to the consecutive vertices of the polygon (Fig. A)
Here, the instruction starts by positioning the first vertex of the polygon at the origin of the reference frame
Axiom: Frame _(0.05),(2){.f(3).-(90)f(3).-(90)f(3).-(90)f(3)}
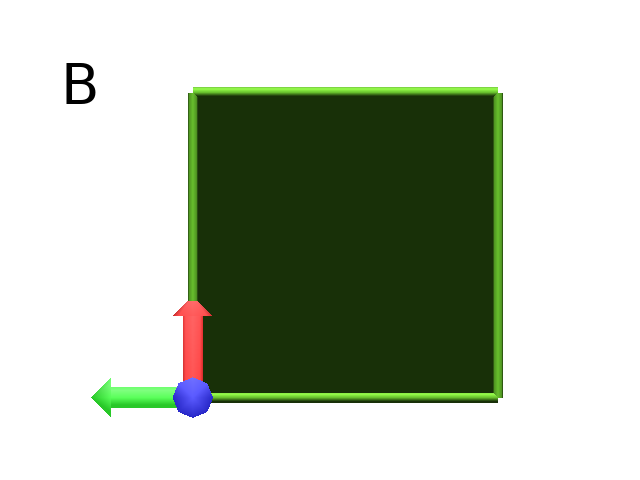
The contour of the polygon can be drawn by using F instead of f. In this case, dots (.) are no longer required after each F (Fig. B)
Axiom: Frame _(0.05),(2){.F(3)-(90)F(3)-(90)F(3)-(90)F(3)}
The number of edges drawn can be different from the number of vertices (Fig. C)
Axiom: Frame _(0.05),(2){.F(3)-(90)F(3)-(90)F(3)}
Note that if the first dot/point is omitted, the polygon is not closed (Fig. D)
Axiom: Frame _(0.05),(2){F(3)-(90)F(3)-(90)F(3)}
Download the example : filledPolygons.lpy
|
|
|
|
Filling concave objects requires to use a smarter filling procedure. This can be acheived by using a True argument to the polygon drawing (by default the argument is False)
# Naive procedure to fill the concave form: (Fig. A)
Axiom: _(0.01),(2) {.F+(95)F(0.7)-(120)F(0.2)+(80)F-(120)F(0.2)+(80)F(0.5)
-(120)F(0.5)+(80)F(0.2)-(120)F(0.5)+(150)F-(120)F(0.3)+(80)F -(120)F+(80)F(0.3)
-(120)F +(150)F(0.5)-(120)F(0.2)+(80)F(0.5)-(120)F(0.5)+(80)F(0.2)-(120)F+(120)F(0.2)
-(150)F(0.7)+(95)F}(False)
# while with a smarter procedure: (Fig. B)
Axiom: _(0.01),(2) {.F+(95)F(0.7)-(120)F(0.2)+(80)F-(120)F(0.2)+(80)F(0.5)
-(120)F(0.5)+(80)F(0.2)-(120)F(0.5)+(150)F-(120)F(0.3)+(80)F -(120)F+(80)F(0.3)
-(120)F +(150)F(0.5)-(120)F(0.2)+(80)F(0.5)-(120)F(0.5)+(80)F(0.2)-(120)F+(120)F(0.2)
-(150)F(0.7)+(95)F}(True)

|

|
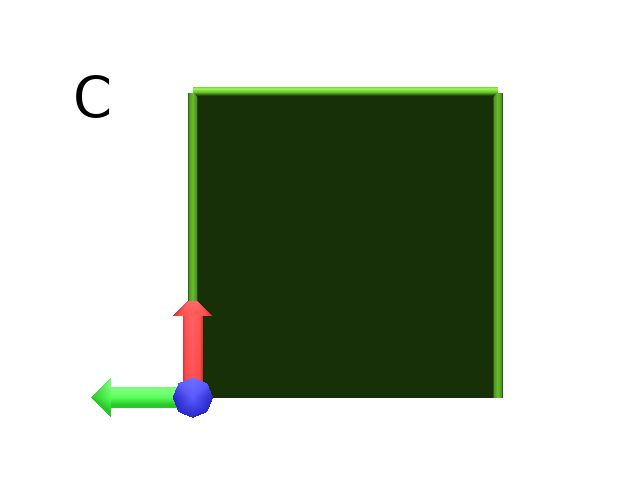
Branching system¶
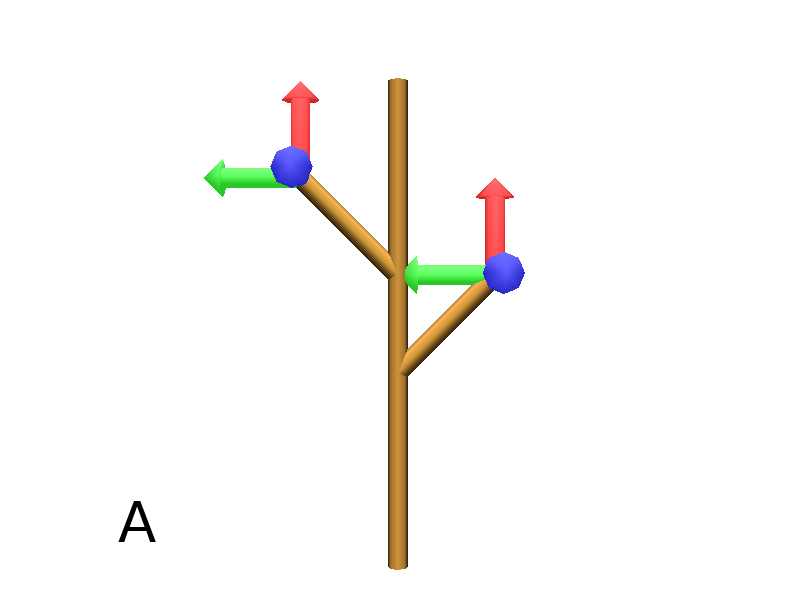
Brackets makes it possible to specify branches. Before each opening bracket, the Turtle’s current arguments (position, orientation…) are stored on the Turtle stack. These arguments are then popped back when a closing bracket is found and the drawing restarts from the popped values.
Axiom: F(4)[+F(3)]F(4) #(Fig. A)
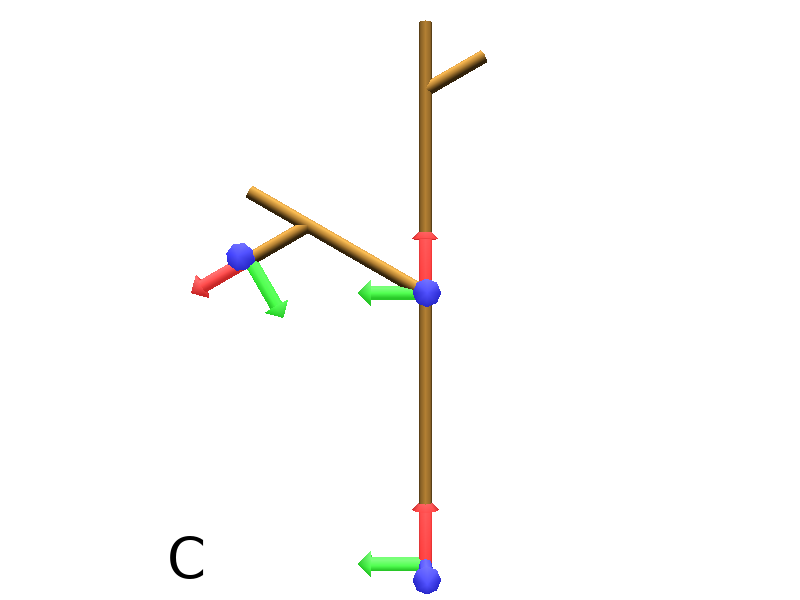
Then it’s possible to nest branches inside each others :
Axiom: F(4)[+F(2)[+F(1)]F(1)]F(3)[-F(1)]F(1) #(Fig. B)
Download the example : branching.lpy
|

|
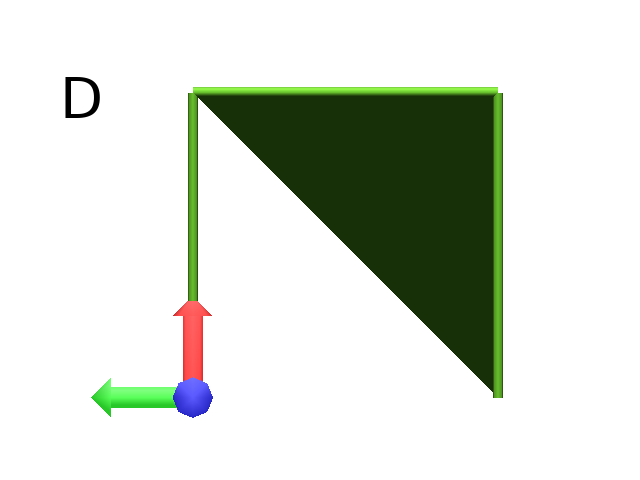
Axiom: Frame F(4)[+F(2)[+F(1)Frame]F(1)]FrameF(3)[-F(1)]F(1) # New code with Frames (Fig. C)
|
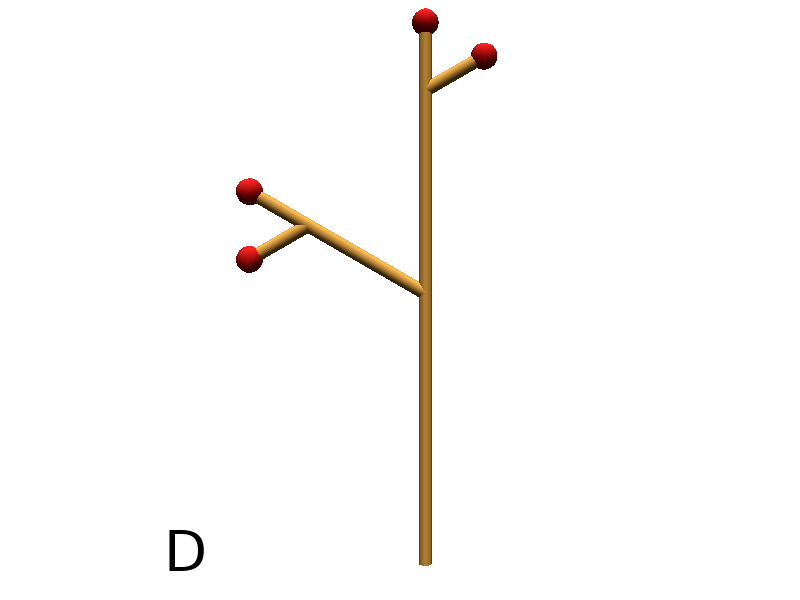
|
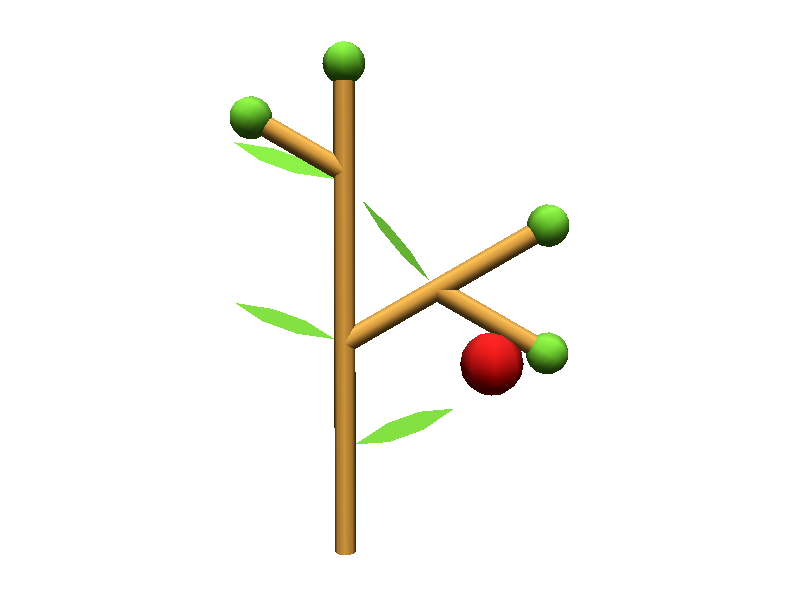
The same branching system can be augmented with other modules (Frame, @O, @B,…) (Fig. D)
Axiom: F(4)[+F(2)[+F(1);(3)@O(0.2)]F(1);(3)@O(0.2)]F(3)[-F(1);(3)@O(0.2)]F(1);(3)@O(0.2) #(Fig. D)
A more complex combined shape¶
There is below a more complex shape using the previous primitives. In this example, ~l is used. This primitive draws a leaf.
Axiom: F[;-(70)f(0.1)\(80)~l]F[;+(70)f(0.1)/(80)~l][-F[;+(70)f(0.1)~l][F(1.2);@O(0.2)]-F(0.6)[-f(0.4);(3)@O(0.3)]F(0.6);@O(0.2)]
F(1.5)[;+(70)f(0.1)/(70)~l]F(0.1)[+F;@O(0.2)]F;@O(0.2)
Download the example : harderExample.lpy
|
Advanced primitives¶
Moving the Turtle¶
There are some primitives which can be used to change the Turtle’s position.
MoveTo and MoveRel¶
@M (or MoveTo) moves the Turtle to the position given in by its arguments. It can be three floats or a vector.
Axiom: @M(0,2,0) Frame #(Fig. A)
import numpy as np
v = np.array([0,1,1])
Axiom: MoveTo(v) #(Fig. B)
Download the example : movement.lpy
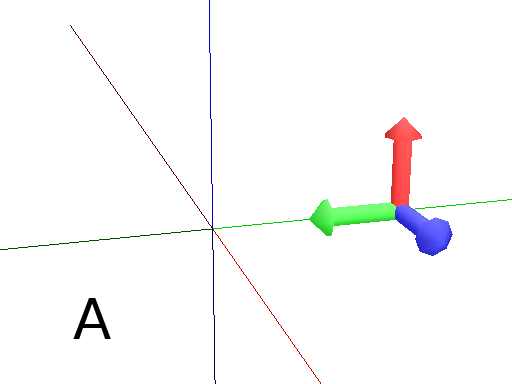
|
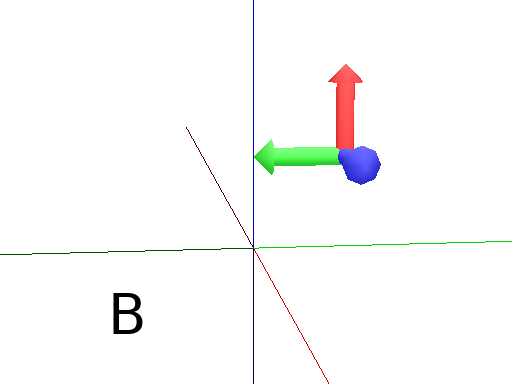
|
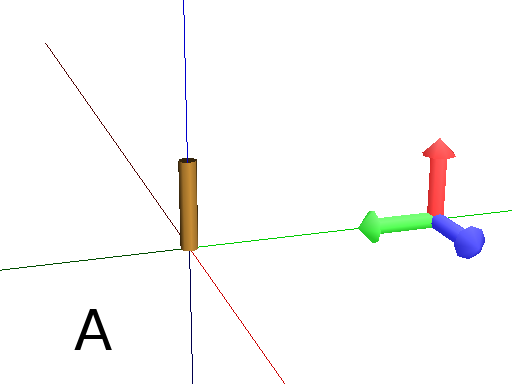
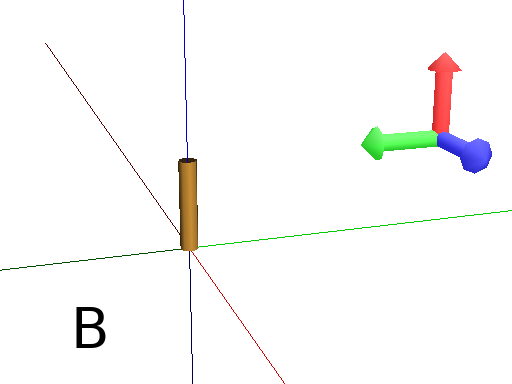
MoveRel works almost in the same way but it moves the Turtle relatively to the current position :
Axiom: F MoveTo(0,3,0) Frame #The Turtle moves to the position (0,3,0) (Fig. A)
Axiom: F MoveRel(0,3,0) Frame #The Turtle moves along the Y axis for 3 units (Fig. B)
|
|
Orient the Turtle¶
The Turtle’s orientation can be set using some primitives.
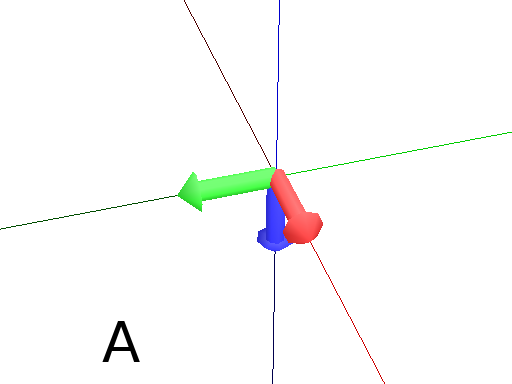
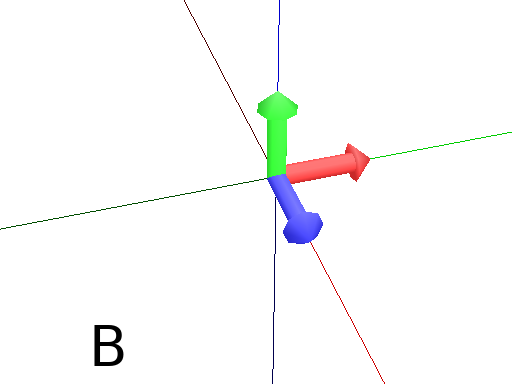
Pinpoint and PinpointRel¶
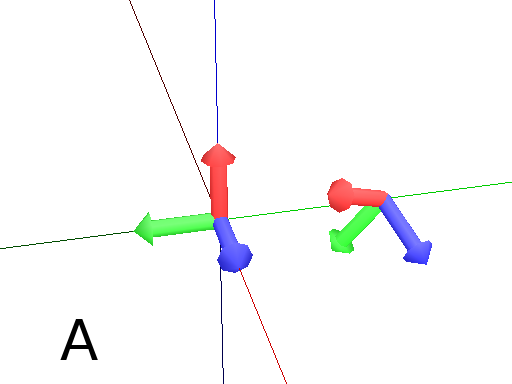
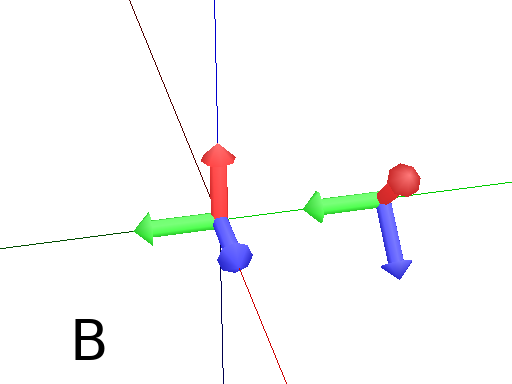
Pinpoint orients the Turtle towards x,y and z given in arguments. It means that the H axis (the red arrow) will point to the coordinates given. One can use also a vector.
Axiom: Pinpoint(1,0,0) Frame # The H axis point to (1,0,0) (Fig. A)
import numpy as np
v = np.array([0,1,0])
Axiom: Pinpoint(v) Frame # The H axis point to (0,1,0) (Fig. B)
Axiom: Pinpoint(1,1,0) Frame # The H axis point to (1,1,0) (Fig. C)
Download the example : orientation.lpy
|
|
|
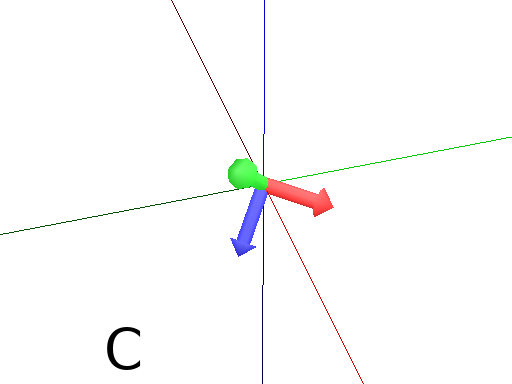
Such as MoveRel for position, PinpointRel orients the Turtle relatively to the current position.
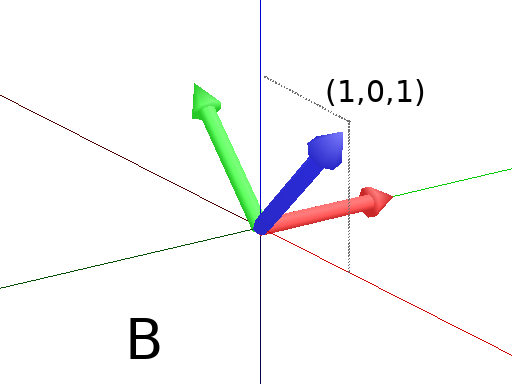
Axiom: Frame MoveTo(0,2,0) Pinpoint(1,0,1) Frame #(Fig. A)
Axiom: Frame MoveTo(0,2,0) PinpointRel(1,0,1) Frame #(Fig. B)
|
|
Setting the HLU axis¶
The H and U axis can be set directly using @R (or setHead). The arguments needed are 6 floats (which represent the coordinates of the two axes) or two vectors.
Axiom: Frame(2) @R(0,0,1,0,1,0) Frame(2) #(Fig. A)
import numpy as np
h = np.array([0,1,0])
u = np.array([1,0,1])
Axiom: Frame(2) @R(h,u) Frame(2) #(Fig. B)
Download the example : setHLU.lpy
In (Fig. A), the H axis point now to (0,0,1) but it was already the case and the U axis point now to (0,1,0). In (Fig. B), the H axis point now to (0,1,0) and the U axis point now to (1,0,1).
|
|
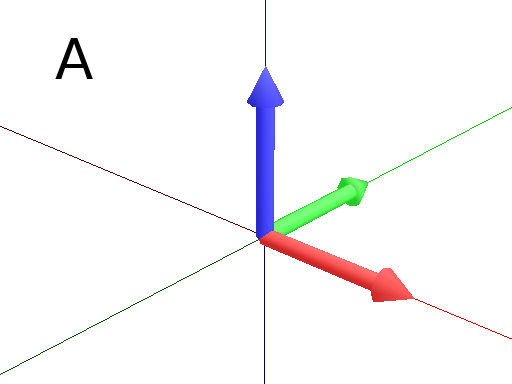
Finally, the Turtle’s orientation can at any moment be set using Euler angles with the primitive EulerAngles. The Euler angles are defined with respect to the other global reference frame (screen coordinates). By default, the initial Turtle’s frame is defined by the Euler angles (180,90,0) with respect to the original frame.
Axiom: Frame(2) EulerAngles(0,0,0) Frame(2) # Turtle’s frame corresponds to the global reference frame. (Fig. A)
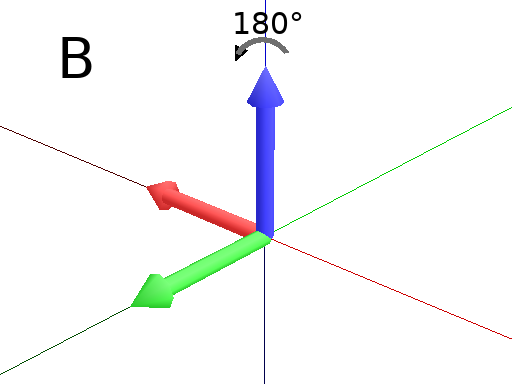
Axiom: Frame(2) EulerAngles(180,0,0) Frame(2) #180° rotation arround Z axis. (Fig. B)
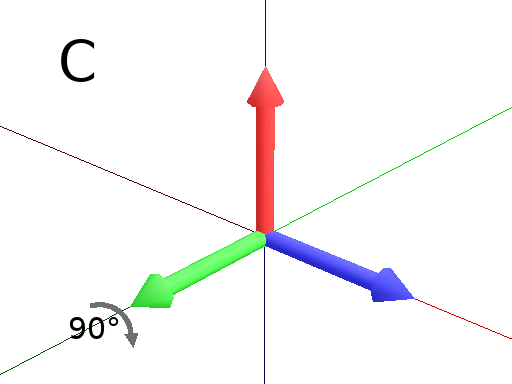
Axiom: Frame(2) EulerAngles(180,90,0) Frame(2) #The 90° rotation arround the new Y axis. (Fig. C)
#There is the initial Turtle's frame
|
|
|
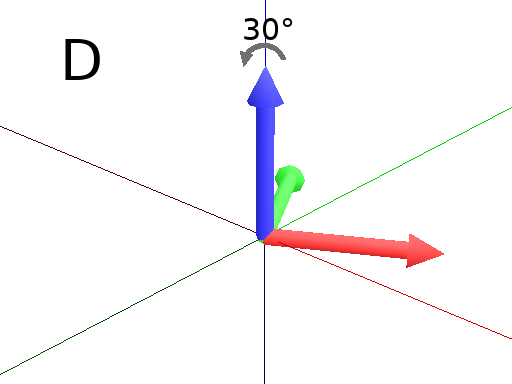
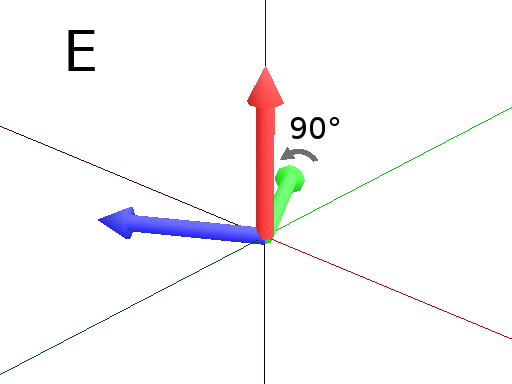
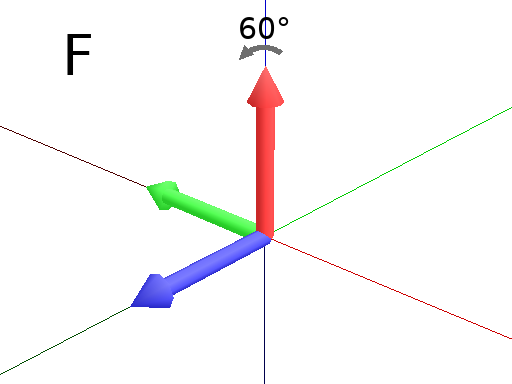
#A succession of 3 rotations : First 30° arround Z axis (Fig. D), then 90° arround the new Y axis (Fig. E)
#and finally 60° arround the new X axis. (Fig. F)
Axiom: Frame(2) EulerAngles(30,90,60) Frame(2)
|
|
|
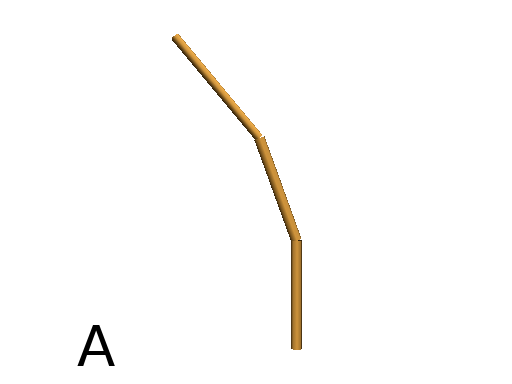
Long path¶
The primitive nF draws n steps of cylinders (n is the first argument). The size can be passed as a second argument.
Axiom: nF(2,1)+(20)nF(2,1)+(20)@D(0.8)nF(3,1) #(Fig. A)
#Equivalent to FF+(20)FF+(20)@D(0.8)FFF
#It can be used to create branching shapes too.
Axiom: nF(2,1)[+(45)nF(2,1)]nF(1,1)[-(45)nF(2,1)]nF(2,1) #(Fig. B)
Download the example : longPath.lpy
|
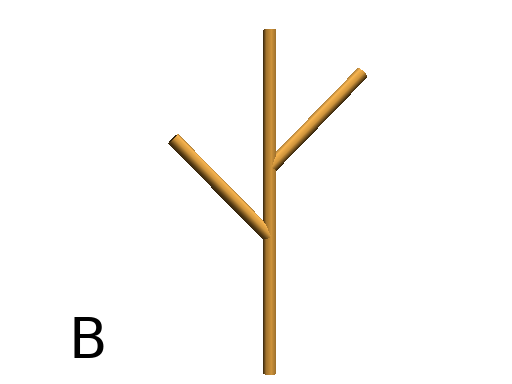
|
Drawing lines¶
The primitive LineTo allows to draw a cylinder from the current position of the Turtle to coordinates given in arguments. The topdiameter can also be given as a fourth argument. Such as other primitives using coordinates, a vector can be used.
Axiom: LineTo(0,0,3)[LineTo(0,1,4)]LineTo(0,0,5) #(Fig. A)
Notice that +, -, / and other rotation primitives don’t have any incidence on LineTo.
Axiom: LineTo(0,0,3)[+(90)LineTo(0,1,4)]-(30)LineTo(0,0,5) #(Fig. B)
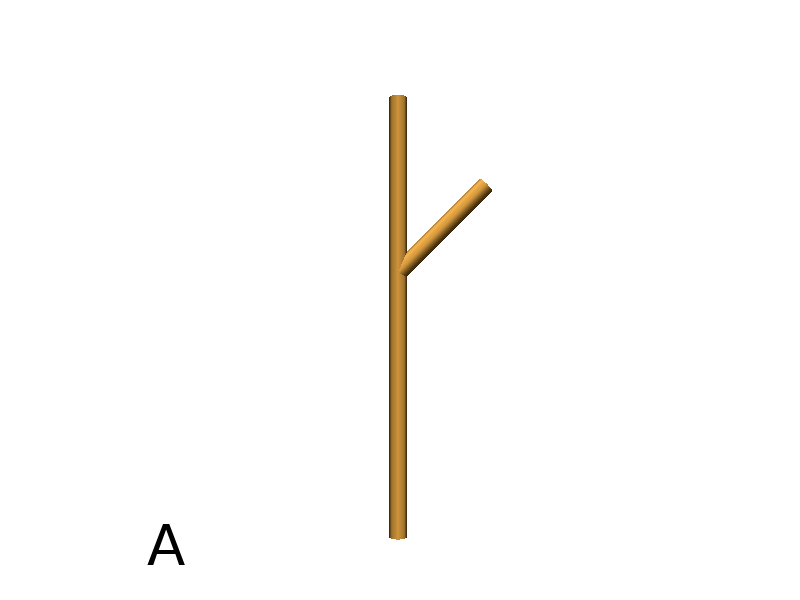
|
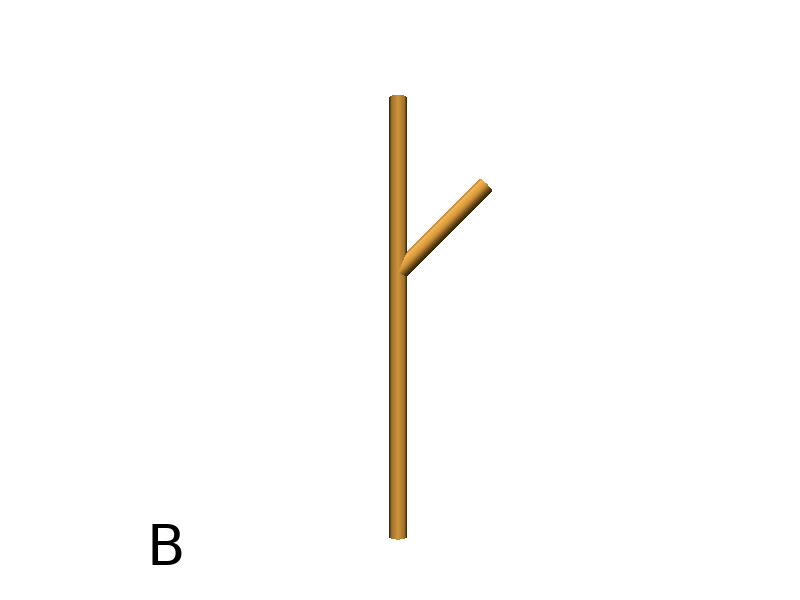
|
LineTo conserve the Turtle’s orientation. To change orientation while drawing, OLineTo should be used.
Axiom: LineTo(0,0,2)[LineTo(0,1,3)Frame]LineTo(0,0,3)[LineTo(0,-1,4)Frame]LineTo(0,0,5) #(Fig. A)
Axiom: LineTo(0,0,2)[OLineTo(0,1,3)Frame]LineTo(0,0,3)[OLineTo(0,-1,4)Frame]LineTo(0,0,5) #(Fig. B)
Download the example : LineTo.lpy
|
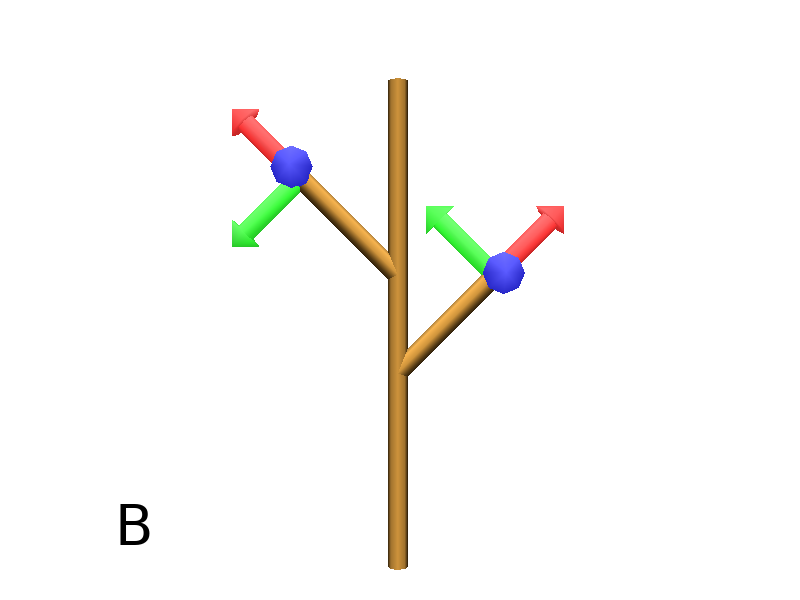
|
A relative drawing alternative also exists for LineTo and OLineTo. These primitives are LineRel and OLineRel
Axiom: LineTo(0,0,2)[LineTo(0,1,2)]LineTo(0,0,4) #(Fig. A)
Axiom: LineTo(0,0,2)[LineRel(0,1,2)]LineTo(0,0,4) #(Fig. B)
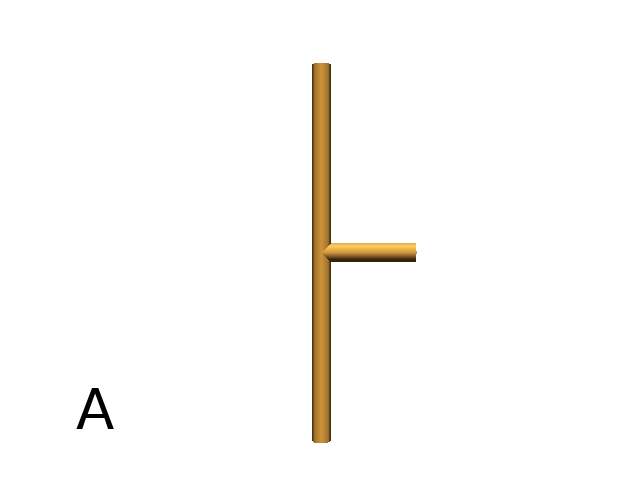
|
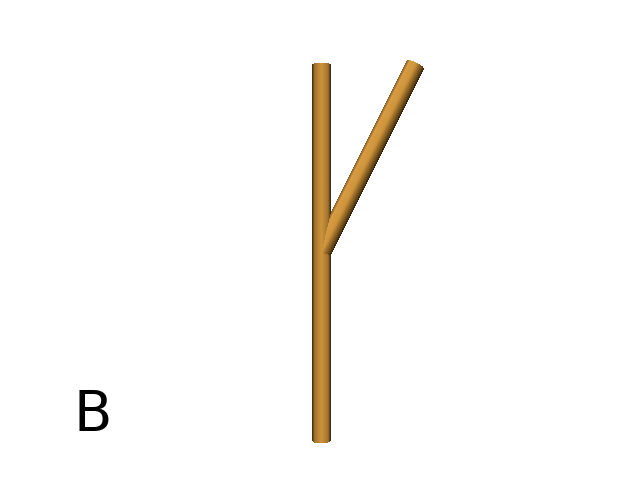
|
SetGuide¶
Drawing a straight line made of length l=10 with segments of size dl = 1.0 (and thus contains n= 10 segments)
Axiom: nF(10, 1.) #(Fig. A)
By adding the primitive SetGuide before the line drawing, it is possible to specify a curve on which the Turtle is moving (instead of heading straight).
The SetGuide primitive must be given two mandatory arguments: a curve (Polyline2D or NurbsCurve2D) and a length: SetGuide(C0, L0). This means that, following this statement, the Turtle will move on curve C1 that has been rescaled from C0 so that its new length is L0 (whatever its original length).
The guiding curve can be defined in different ways. It can be defined for example by a python function (function f defined hereafter), e.g. (Fig. B) :
from openalea.plantgl.all import Polyline2D
from numpy import arange
def f(u):
return (u,u**2)
C0 = Polyline2D([f(u) for u in arange(0,1,0.1)]) # (Fig. B)
Then using curve C0 in the SetGuide primitive, one can move the Turtle over a cumulated length L, thus using the defined curve C1 (rescaled from C0) as a guide for moving up to a total length L0:
L = 10
L0 = 10
Axiom: SetGuide(C0,L0) nF(L, 0.1)
Download the example : setGuide1.lpy (With a Polyline2D imported from PlantGL)
|
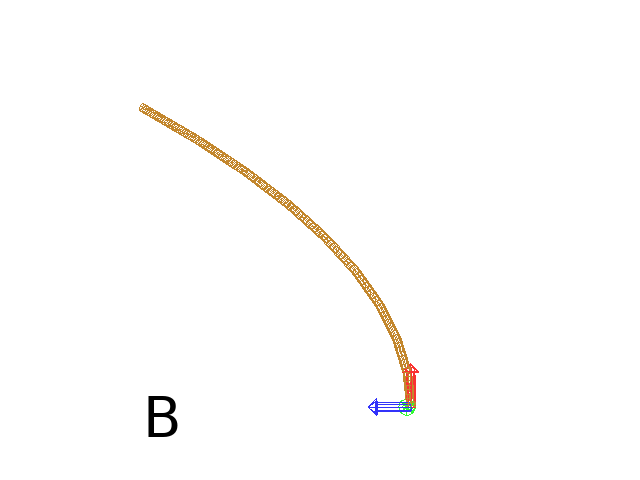
|
or like the (Fig. C) example, the embedded L-Py graphical interface can be used to specifying 2D curves (the curve is then given the name C0 for instance in the interface):
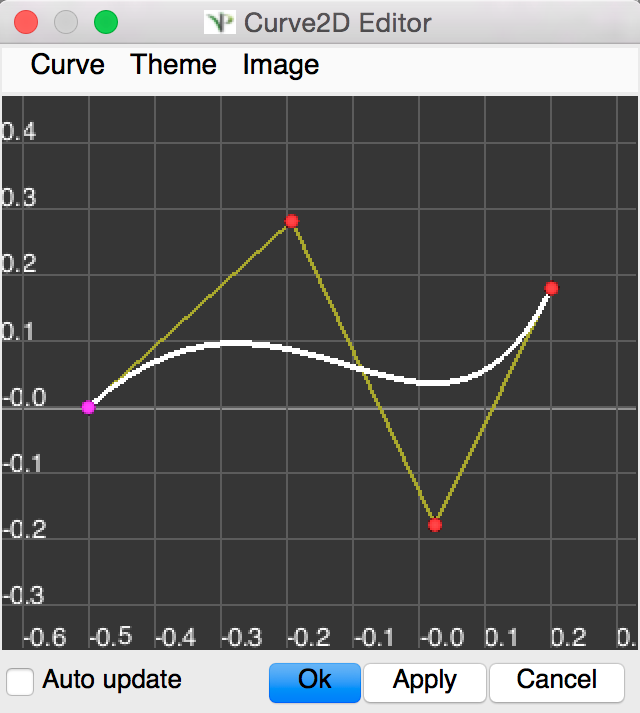
|
|
Download the example : setGuide2.lpy (With a Polyline2D created in the L-Py graphical interface)
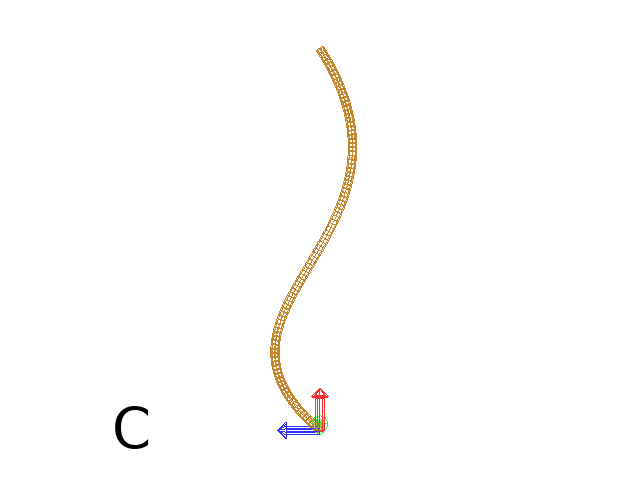
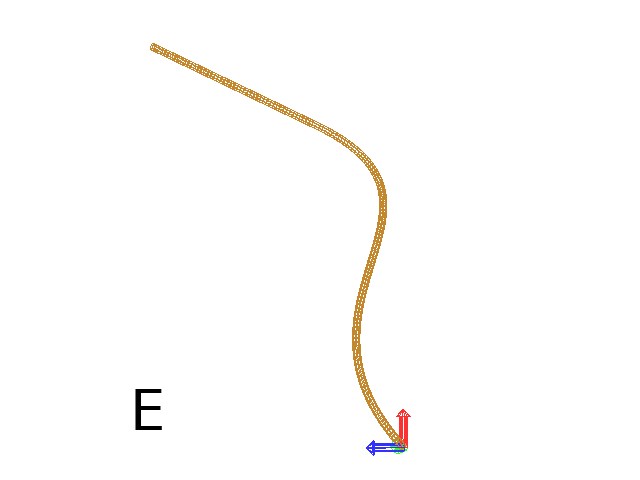
Note that the Turtle can move less than the length of the 2D curve. In this case it will proceed forward over the L first units at the beginning of curve C1 (Fig. D). By contrast, if L > L0, then the Turtle keeps on moving straight after reaching length L0 (E).
L = 6
L0 = 10
Axiom: SetGuide(C0,L0) nF(L, 0.1) # (Fig. D)
L = 15
L0 = 10
Axiom: SetGuide(C0,L0) nF(L, 0.1) # (Fig. E)
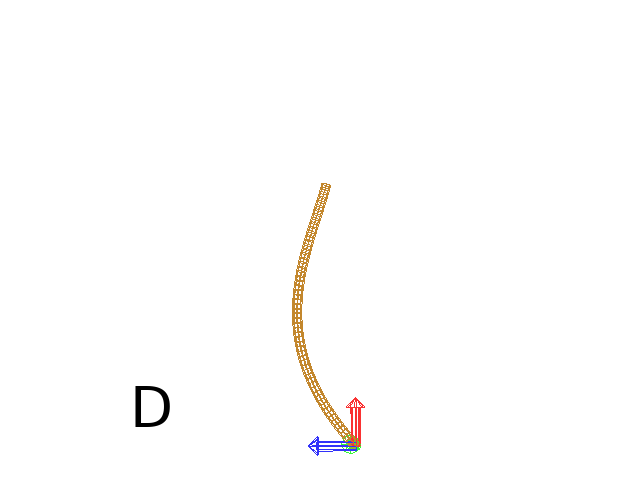
|
|
To stop using the 2D curve as a guide, EndGuide can be used.
Generalized cylinders¶
When several rotations are used while drawing, the rendering at rotation places isn’t great. The separation points are really visible. To fix it, @Gc (or StartGC) can be used. Until a @Ge (or “EndGC”) all shapes drawn will be merged so that it becomes only one shape.
Axiom: F(2)+(30)F+(30)F+(30)F+(45)F+(45)F@O #Cylinders not generalized (Fig. A)
Axiom: @GcF(2)+(30)F+(30)F+(30)F+(45)F+(45)F@O@Gc #Cylinders generalized (Fig. B)
Download the example : generalizedCylinders.lpy

|
|